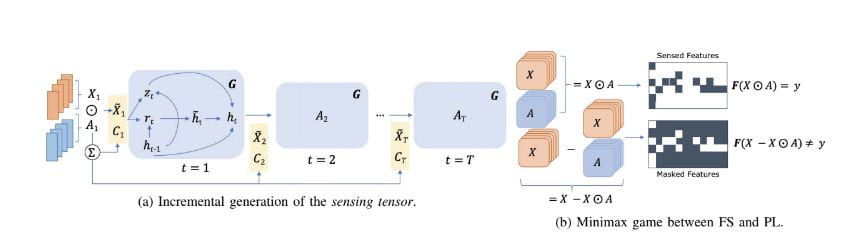
For many real-world tasks obtaining a complete feature set is prohibitively expensive, especially in healthcare. Specifically, physicians must constantly balance the trade-off between predictive performance and cost for which features to observe. In this paper we tackle this problem by proposing precision sensing, formulating it as a time-dependent resource distribution problem described by a two-player minimax game between a dynamic feature sensor (FS) and a progressive learner (PL). FS delivers an online sensing strategy that is adaptive to budgetary constraints on feature observations. The PL allowsthe FS to adapt its sensing strategy by learning to handle progressively sparser sets of features. We prove the existence of Nash Equilibria in the proposed formulation and provide an initialization scheme to find one. We also show how the proposed framework can be applied to a real-world healthcare setting. Empirical results show that models conditioned on the sensed data maintain competitive predictive power, despite sensing only a fraction of the features across time.
AI Reading Group 15/Apr/2021: Adversarial Precision Sensing with Healthcare Application
